はじめに
こんにちは、意識低い系ミュージシャンの龍ちゃんです。
「楽に音楽をする」をモットーに音楽に関する情報を発信しています。
(バックナンバーの「相対的な見方が大事」を読んでから本記事を読むことを強く推奨します)
音楽理論学習の最も難しいところとして、「専門用語が多いこと」が挙げられます。
多いだけなら頑張ればいいのですが、それぞれがかなり複雑な概念でして、とある専門用語を理解するのに別の専門用語が必要で、また別の専門用語も必要で…のようなことが起こるのです。
「オシャレな服を買いに行くためのオシャレな服がない」状態です。
実は音楽理論を学び音楽を楽に楽しくできるようになるためのハードルの高さは、この専門用語の理解がほとんどです。
ここを乗り越えられれば、それだけで音楽のレベルが格段に上がります。
簡単ではありませんが、しっかり読み込めば必ず理解できます。
頑張っていきましょう。
どこから説明すればいいかというのは本当に悩みました。
一番良いのは専門用語の記事をそれぞれ何度も行き来して納得いくまでじっくり向きあってもらうことなのですが、そうは言っても順序は必要です。
悩んだ結果、まずは音と音の距離を示す「音程」という専門用語の解説を行います。
この記事一つだけで完全な理解ができるほど簡単なものではありませんが、極力わかりやすく書いていきます。
もしこれだけ読んで腑に落ちなくても、次回以降の専門用語記事を読んでいって、もう一度戻ってくれば理解がより深まると思います。
音程とは?
早速「音程」という専門用語について解説していきます。音程とは、言い換えると「音と音の高さの差」です。
前回の記事でお伝えした通り、音楽において大事なのは「相対的な見方」、すなわちとある音楽における基準がどこかを知覚することや、その基準からどれだけ離れているかを知覚することです。自分がジェットコースターのどのあたりにいて、クライマックスまでどのくらいか…といったことを認識するのが大事です。
それには当然、音と音の差を認識するための指標が必要になりますよね?音がそれぞれ単品で自分の前にあっても、基準がどこか、などという情報は生まれません。
音と音の差を認識するための要素が今回紹介する「音程」です。
早速一例を見てもらいましょう。
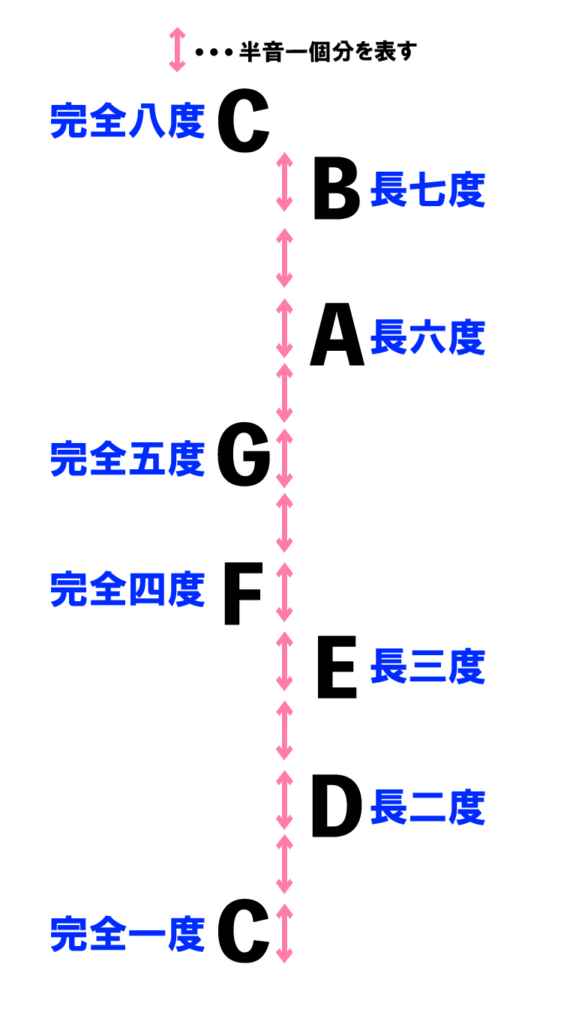
こちらに示したのは「Cメジャースケール」というスケールです。ここで早速出ました。
「専門用語を理解するのに専門用語が必要」現象です。
今回スケールという専門用語について解説しているとボリュームが膨大になってしまうので、今は「この順番で音が並んでいるとCメジャースケールと呼ばれるのだな」ぐらいにとらえてください。
また補足としてもう一点。
私の書く記事で音そのものについて言及するときはドレミファソラシドではなく英語音名を使います。理由として、そちらのほうがコードを扱うときにスムーズであるのと、相対音高と絶対音高を区別するためです。(これらの用語についてわからなくても今は大丈夫です)
さて、このCメジャースケールがどんなものかは置いておいて、これはあらゆる音楽理論の基準になっている音の並びです。(「長」とか「完全」とか名前がついているのは一度無視してください。)
音程は「度」で表されます。
Cから数えてCは一番目(ゼロではないことに注意)、Dは二番目…という数え方で「度」がついています。
一度の存在に関してはビルを想像するとわかりやすいかもしれません。ビルに0階はないですよね。
次に、一旦は無視してもらっていた、なにやら頭にくっついている漢字について。
雑な説明をしてしまうと、「1,4,5,8は完全」「2,3,6,7は長か短」という具合になります。
「長5度」とか「完全3度」はありえないんです。
ただ厄介なのが、のちに出てくる「減5度」とか「減3度」は両方あり得るということなんです。
ここが大混乱ポイントです。
では一体どういうメカニズムでそれらの接頭語が決まったのかを見ていきましょう。
音程のグループ分け
「完全」と「長、短」が区別されている理由をまず知りたいところだと思います。実はそれぞれの音の聞こえ方が大きくかかわってきます。
突然ですが、「不協和音」という言葉を耳にしたことはありますよね?
「聴いていてなんとなく気持ち悪い和音」ぐらいの認識は誰でも持っているかもしれません。では「聴いていて気持ちいい和音」との差はなんでしょうか?考えてみれば、同じ「和音」という現象なのにこうも聞こえ方が違ってくるのは不思議です。
何となく気持ちいいのと何となく気持ち悪いのを交互に並べてみました。
さて、音程が音の聞こえ方に影響を及ぼすメカニズムを見ていきましょう。
音程とは音と音の高さの違いです。そもそも「高さ」とは何か。中学校の理科で習いますが、「周波数(一秒に何回振動するか)」です。
つまり音程とは空気の振動の周波数の違いであるということになります。周波数の違いといっても「差」ではなく「比」になります。
和音が鳴っているときというのは、高さが違う二つの音が鳴っている、つまり違う周波数の波が同時に振動しているということになります。
二つ以上の波が同時に発生すると「干渉」と呼ばれる現象が起こり波の形が変化するのですが、実は「聴いていて気持ちいい和音」では、二種類の周波数の比が単純なので、干渉した後の波がキレイな形になるんです。
干渉してもキレイな形になる音と音の比、つまり音程のことを「協和音程」と言います。
その逆、聴いていて何となく気持ち悪い音程のことを「不協和音程」と言います。
「不協和音」とは、「不協和音程により構成された和音」ということですね。
さて、周波数の比が簡単なものが協和音程と呼ばれることはわかりました。実はその協和音程の中にもさらに比が簡単、つまり干渉した波がより綺麗な形になるグループと、そうでないグループに分かれます。
より簡単な方が「完全協和音程」、そうでないほうが「不完全協和音程」と呼ばれます。
この「より簡単なグループ=完全協和音程」が、「1.4.5.8度」つまり接頭辞に「完全」がつくものになります。
一方、そうでないが協和音程には属しているもの=不完全協和音程が「3.6度」です。
残る「2.7度」は比が簡単なグループからは外れるので、「不協和音程」です。
これらのグループ分けがわかったうえで、音程の名前に関するさらなる法則をみていきましょう。
接頭語変化の法則
勘のいい方はお分かりかもしれませんが、「音程」とは音と音の距離なので、Cから他の音、という数え方だけでなく例えばDとGの音程、BとCの音程、なども当然存在します。
先ほどの画像の段階では「長」と「完全」しか接頭語が存在しませんでしたが、それ以外のものがここで出てきます。
まず例としてFとBの音程をみていきましょう。
一見、「Fから数えてBは4番目で、4度。→4度は普通完全がつくので、この二つの音程は完全4度。」というように推測できるように思えます。
ですが、実はこの音程は少し特殊なところがありまして、他の四度に比べて「半音一つ分」広いんです。「半音」とは音の高さの最小単位で、ピアノの鍵盤一つ分、ギターのフレット一つ分に当たります。
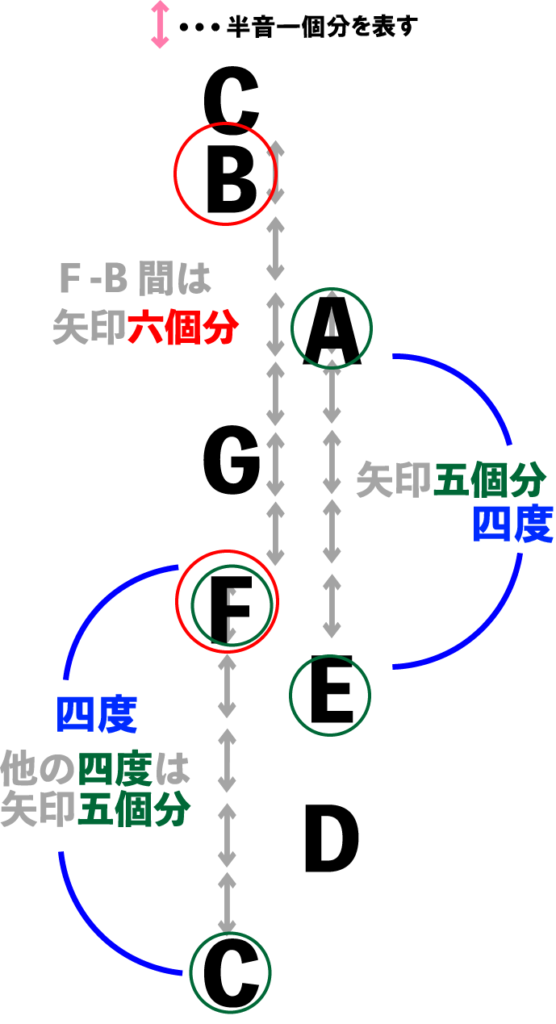
このFとBのように完全四度と比べて半音一つ広い音程のことを、「増四度」といいます。
四度に限らず、「完全」という名前の付く音程、つまり完全協和音程に対して、その音程が半音一つ広くなったら「増」、反対に半音一つ狭くなったら「減」が、「完全」の代わりに接頭語としてつきます。
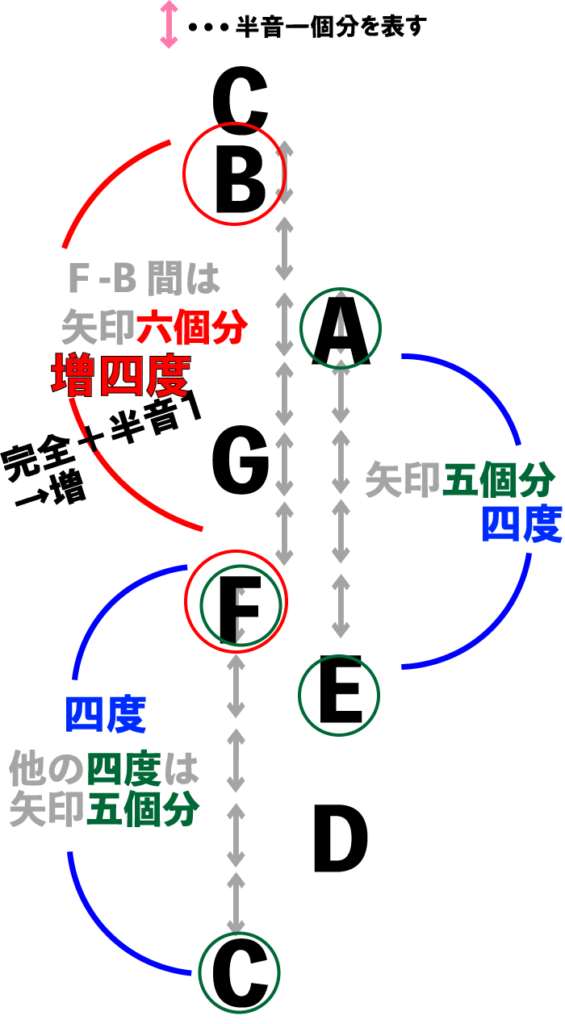
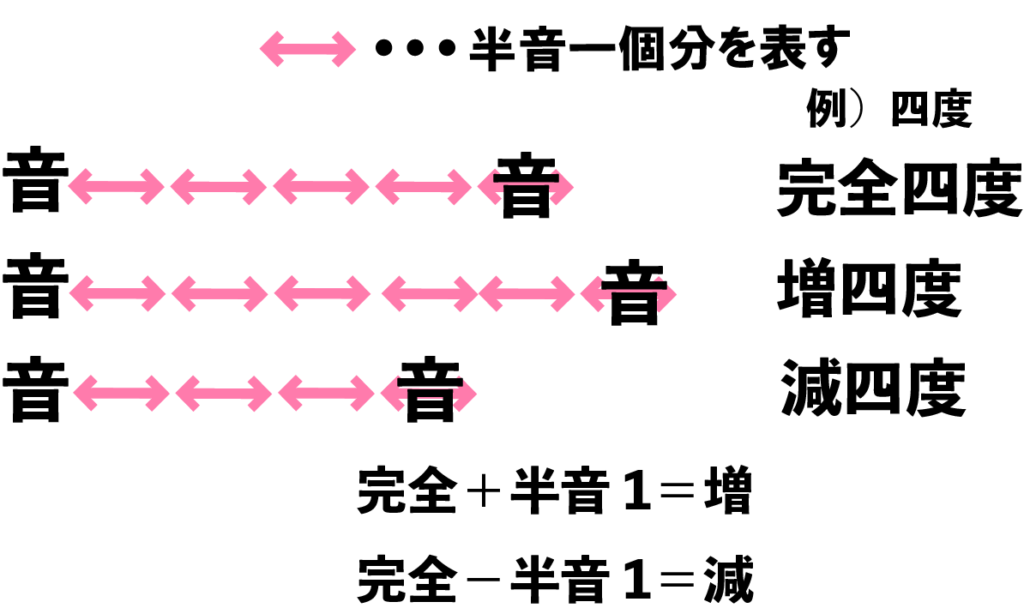
次に、残りの不完全協和音程、不協和音程について見ていきましょう。
例として、AとCの音程を見ていきます。
AとCの音程は「三度」であり、一でも四でも五でもないので、接頭語として「完全」がつくことはありません。接頭語を決めるために、他の三度を参考にしてみましょう。CとEの音程を見直したら「長三度」と名付けられています。
Aから数えてCは三番目、だから同じく長をつけて「長三度」!…とはいかせてくれません。
CとEの距離、長三度に比べて、AとCの間はは半音一つ分狭くなっています。
じゃあ先ほどの例にのっとって「減三度」!…というわけでもありません。
「長」という接頭語をわざわざつけるぐらいならその逆の「短」があることも想像がつきますよね。「長」がつく音程に比べて半音一つ分狭い音程の接頭語は「短」になります。
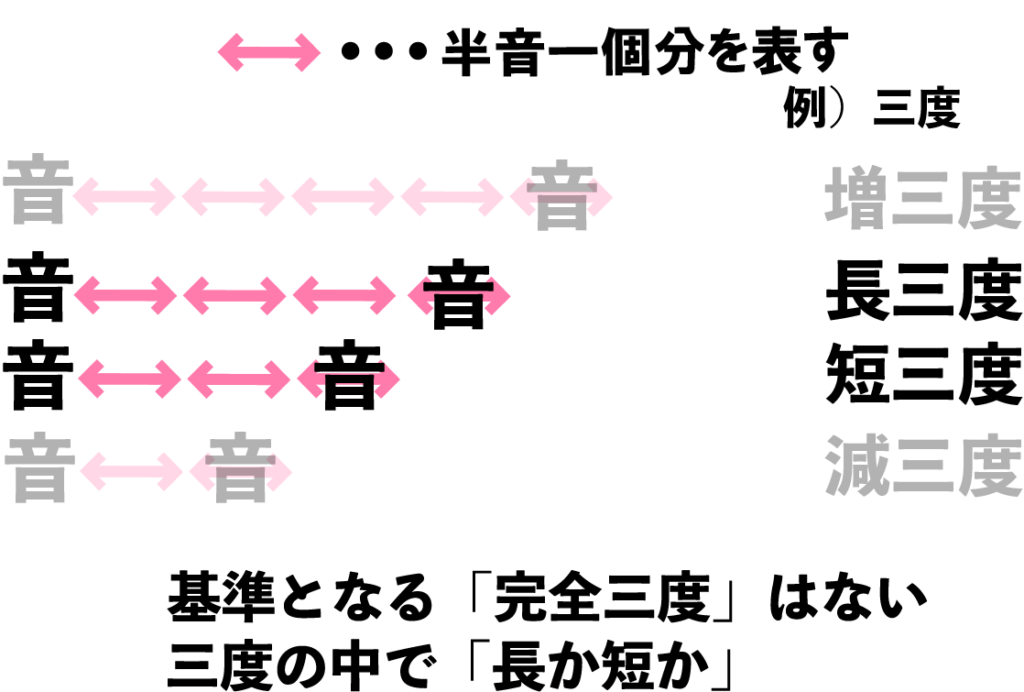
この短からさらに狭まった場合「減」が付きます。反対に、長から半音一つ広がった場合、「増」が付きます。
(「減三度」「増三度」など、不完全協和音程や不協和音程の増減は理論上は存在しますがほぼ使うことはないです)
音程の名前を確定させる手順を整理します。
- まず“音名で”音と音がいくつ離れているかを数えます。この時点で「度」が確定します。
- 「『完全』や『長』がつく音程に比べて半音一つ分狭いか広いか」を見て、接頭語が確定します。
(この音程の名前の決め方については実践を見ていただくのが最も良いと思うので、今度解説用のコンテンツを補完しようと思います。)
ここで注意してほしいのが、この手順でのみ名前が確定するということです。
手順2だけ、つまり半音いくつ分離れているかだけで音程の名前を確定させることはできないのです。
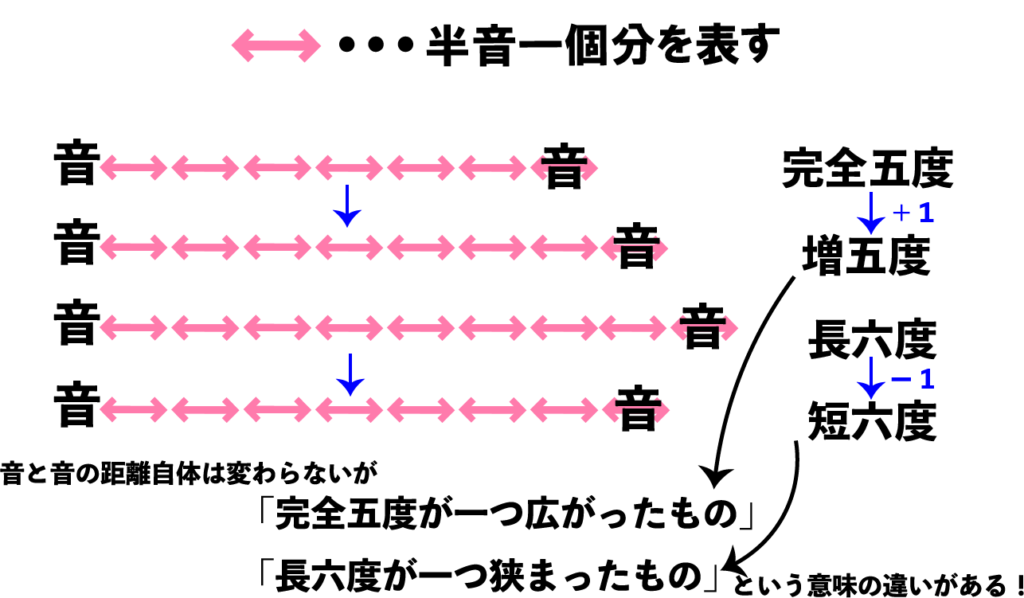
この二つは半音で高さの差を表すと全く同じ数になるのですが、音楽の中での意味は全く異なるものになります。
半音でいうと同じ差ですが、「完全五度が半音一つ広がった音程」「長六度が半音一つ狭まった音程」この二つの意味は明確に異なりますし、曲の中で聴いても確かに違う情緒をもって聞こえます。ここが音程という概念の非常にややこしいところです。
スケールの流れがあって初めて音程というものが決まります。音程を単品で聴いても差はわからないのですが、実際に曲の中で流れとともに聞いてはじめてその差がわかります。
♪♪♩♩というリズムのメロディをつくりましたが、各フレーズの最後から2番目の音が前半はCメジャースケールの「増五度」の音、後半は「短六度」になっています。音自体の高さ、Cという基準からの距離は全く変わらないのですが、ニュアンスの違いがよくわかると思います。
音楽理論を数学のようなものとしてとらえていると「半音いくつ分か」というデジタルな情報のみを求めてしまいがちですが、そういった音程のとらえ方は意味を成しません。
あくまで「スケール上でいくつ離れているか」という情報があって初めて、音程という情報は機能するのです。
この注意点に関してはこの段階で必要性を理解するのが非常に難しいので、今はとにかく音程を確定させる手順を守るようにしてくれれば大丈夫です。
音程という概念に慣れるために練習問題をやってみましょう。
- GとDの音程は?
- DとFの音程は?
- CとG#の音程は?
- EとDの音程は?
なお、これらすべて基準の音のほうが低いものとします。
挫折を防ぐために重要なので何度も繰り返します。「音と音の高さの差」、つまり音程は音楽を見ていく上で非常に重要な概念ですが、その差を「半音いくつ分離れているか」で表すことはできません。
”音名でいくつ離れているか”という点が非常に重要です。
まとめ
さて、音楽を見ていく上で大事な「相対的な見方」を支える「音と音の高さの差」、それを表すものとして「音程」という専門用語を解説しました。
今回解説したのは高さの差に名前を付ける方法までです。
具体的にそれぞれの高さの差にどのような意味合いがあるのかということは今後解説していきます。
音楽を構成する要素を解説するのに最も大事な専門用語になりますので、先を急がず、まずはここを理解してください。
この基本を理解できるかどうかで、音楽を楽に楽しくできるかどうかが決まってきます。
次回はスケールについて解説していきます。
【練習問題の答え】
- Gを基準としてG→A→B→C→Dでまず「五度」が確定します。五度は基本的な接頭語が「完全」であり、半音で見ると元の音を含めずに7つ分離れています。GとD間を半音でみていくと、G#、A、A#、B、C、C#、Dとなり、半音7つ分離れているので、「完全五度」で確定します。(五度、四度に関しては、増や減のケースの方がレアなので、そちらの組み合わせを覚えてしまい残りは完全、としてしまう方が効率が良いです。)
- Dを基準としてD→E→Fでまず「三度」が確定します。三度は元の音を含めずに半音4つ離れていたら長、3つ離れていたら短になります。DからFまではD#、E、Fと、半音三つ分離れているので、「短三度」になります。
- Cを基準としてC→D→E→F→Gでまず「五度」が確定します。#を無視して単純な「音の名前」で度数の部分が決まることに注意してください。CとGは完全五度離れていることはCメジャースケールの図を頭に入れていればすぐでてきます。そのうえで、G#、つまり半音一つ分完全五度から広くなっているので、「増五度」になります。
- Eを基準としてE→F→G→A→B→C→Dでまず「七度」が確定します。ここで一つ裏ワザ的なものを紹介しましょう。Cメジャースケールの長七度を観察すると、主音の半音下のオクターブ上になっています。つまりEからの長七度というのはEの半音下のオクターブ上、つまりD#になります。よって、Eに対するDとの間隔は長七度より半音狭くなります。つまり「短七度」です。
用語解説に関する記事をもっと読む
記事が見つかりませんでした。



